Propane Characteristics and Performance in Hot Air Balloons

Frank M. Bacon

May 21, 2014

fmbacon@comcast.net

Introduction

This study was initiated after hearing about a hot air balloon accident described at our local balloon safety seminar on March 22, 2014, by Dr. Tom McConnell. The accident involved a hot air balloon descending on power lines as it attempted to land. What caught my attention was that the pilot described his propane levels in the fuel tanks as 15% in one tank and 10% in the other. My experience in flying hot air balloons is that when the fuel is that low the balloon does not respond as well as it does with higher propane levels, and the balloon performance can deteriorate rather quickly at the lower propane levels. My balloon flight manual describes safe operating conditions with propane pressures of greater than 80 psig and less than 160 psig, with marginally safe operations at from 60 to 80 psig, and unsafe operations at less than 60 psig. The flight manual also states, “Ensure that fuel pressure at start of flight will be adequate to allow for pressure decay during flight.” I have only flown with low propane conditions a few times, and these thoughts were based on what I remember. These flights were probably with vapor pilot light configurations. I did not monitor the propane pressure during these conditions as I was too busy flying the balloon.

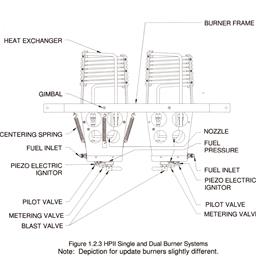
Most of my experience over the forty years of flying balloons has been in balloons with vapor pilot lights, as the balloon involved in the accident was described to have. In these balloons, the pilot light uses vapor delivered through a low-pressure hose from the top of the propane tank. The vapor evaporates from the liquid propane in the tank thus reducing the temperature of the propane due to evaporation. Liquid propane to the burners is delivered from the bottom of the tank through a metal tube inside the tank through a valve at the top of the tank and through a high-pressure hose to the burners. My flying experience since October, 2008, has been with pilot lights that run directly off the liquid delivered to the burners which is converted to vapor at the burner through a vapor converter and regulator; only one high-pressure hose is connected to the tank. This configuration should have a reduced impact on the liquid propane temperature in the tank since pilot-light vapor is not due to evaporation in the tank; temperature reduction of the liquid would only occur due to evaporation of the liquid in the tank to replace the fuel delivered to the burner and pilot. As the following development will suggest, the pilot light configuration could impact the properties of the propane and the performance of the balloon, especially at low propane levels. The main components of the fuel-burner system are shown at the end of this article. The propane tank is made out of 304 and 321 stainless steel.

Hypothesis

As propane is used to heat the balloon, evaporation takes place in the propane tank to replace the quantity of the liquid used, which causes the temperature and pressure of the liquid propane to decrease. As the liquid propane decreases during the operation of the balloon the amount of heat to evaporate the liquid is pulled from a smaller volume of liquid causing a more significant impact on the temperature of the liquid and on the pressure in the tank. Vapor pilot lights would tend to further lower the temperature and pressure of the propane during the balloon flight.

Calculations of Pressure-Temperature Characteristics of Propane Fuel During the Flight of a Hot Air Balloon Assuming Adiabatic Conditions for the Propane

The following theoretical development is based on simple heat transfer calculations. (That is all I know how to do.) The concept is that if a gallon of liquid propane is removed from the tank to power the balloon, a gallon of vapor must be evaporated to fill the space vacated by the liquid requiring heat to be removed from the liquid. The pressure of the propane is determined by the temperature of the liquid and the vapor pressure characteristics of propane. The amount of heat removed from the liquid is dependent on the heat of vaporization and the mass of the propane evaporated. Note that the calculations only relate to evaporation inside the tank; evaporation at the burner is supplied by heat from the burner itself at the heat exchanger and does not impact the temperature of the liquid in the tank. In my initial set of calculations of the pressure-temperature characteristics of the propane in the tank, I assume no additional heat is added to the liquid from other sources. I use the conditions of the balloon that I fly, that is, 15 gallon, stainless steel, propane tanks, which are the same tank sizes in the balloon involved in the accident. The tanks have insulated jackets. As mentioned earlier, the pilot lights in my balloon run off of liquid delivered to the burner through pilot converters. I don’t have data on vapor consumption by vapor pilot lights to consider in my calculations at this point.

For the following calculations, the propane tank has a liquid volume (V_L) – initial value of 15 gal. – and vapor volume (V_V) – initial value of 2.5 gal. As stated above, I assume an adiabatic process, no heat transfer from the outside to the propane. I will calculate the tank pressure as the liquid is reduced in multiple steps of ΔV_L. As the liquid is reduced by ΔV_L, the ΔV_L is filled with vapor by evaporating the liquid; ΔV_L = ΔV_V.

The energy ΔH required to evaporate the necessary liquid to replace the vapor is described by:

(1) ΔH = ΔV_V x ρ_V x H_V

Where ρ_V is density of the vapor

H_V is heat of vaporization

ΔV_V is the volume of vapor necessary to fill the volume of liquid removed.

The reduction in temperature of the propane ΔT_P due to the evaporation is given by:

(2) ΔT_{P =} ΔH / [(V_L - ΔV_L) x C_PL x ρ_L + (V_V + ΔV_V) x C_PV x ρ_V]

Where C_PL is the specific heat at constant pressure for the liquid

ρ_L is the density of liquid

C_PV is the specific heat at constant pressure for the vapor

ρ_V is the density of vapor

I cycled through iterations of the calculations with ΔV_L equal to one gallon per cycle, calculating after each cycle the new temperature of the propane and corresponding pressure in the tank[1]. The tank pressure can be determined from Pressure-Temperature data for propane obtained from NIST tables on the internet at: http://webbook.nist.gov/cgi/fluid.cgi?ID=C74986&Action=Page

The Heat of Vaporization was obtained from “Handbook of Physics and Chemistry” published by the Chemical Rubber Publishing Co. (See Figs. 2 and 3).

These data were fitted with second order polynomial regression trendlines in a Microsoft Excel spreadsheet for use in the calculations; all of the equations fit the data with R² values of at least 0.9997. The parameters of interest:

(3) ρ_V = 0.0054 T² + 0.0.2726 T + 10.446; (T in ^◦C; ρ_V in kg/m³)

(4) H_V = -0.0018 T² – 0.271 T +89.623; (H_V in cal/g)

(5) ρ_L = -0.0051 T² – 1.3215 T + 528.56; (ρ_L in kg/m³)

(6) C_PL = 2e^-5 T² + 0.0016 T + 0.5988; (C_PL in cal/g-^◦C for liquid)

(7) P_V = 0.031 T² + 1.9888 T + 69.151; (P_V is absolute vapor pressure in psia)

(8) C_PV = 3e^-5 T² + 0.0019 T + 0.4168; (C_PV in cal/g-^◦C for vapor)

(9) T_eq = -0.0009 P_V² + 0.5418 P_V – 32.61; (T_eq is equilibrium temperature-^◦C)

For the following calculations, the volume units are gallons.

Figure 1. Heat of Vaporization for Propane

Figure 2 Pressure-Temperature Characteristics of Propane

Following the reduction of the liquid propane by ΔV_L, the heat loss in the liquid propane necessary to evaporate ΔV_V (equal to ΔV_L) gallons of vapor can be calculated by substituting the above equations in:

(10) ΔH_L = 3.79 x ΔV_V x ρ_V x H_V; (ΔH in calories)

The decrease in temperature in (V_L - ΔV_L) gallons of liquid becomes:

(11) ΔT_{P =} ΔH_L / [3.79 x {(V_L - ΔV_L) x C_PL x ρ_L + (V_V + ΔV_V) x C_PV x ρ_V}]; (ΔT_P in ^◦C)

The new temperature of the propane is then given by

(12) T_P2 = T_P1 - ΔT_P

The resulting equilibrium vapor pressure can then be calculated by:

(13) P_V2 = 0.031 (T_P1 - ΔT_P)² + 1.9888 (T_P1 - ΔT_P) + 69.151

where T_P1 is the initial temperature of the propane.

The gauge pressure, P_G, is calculated by subtracting the absolute ambient atmospheric pressure of 12.5 psi from the absolute pressure P_V; 12.5 psi is the atmospheric pressure at Albuquerque’s altitude above sea level.

The reduction in the volume of liquid due to the evaporation, ΔV_LE, of ΔV_V gallons of vapor is given by

(14) ΔV_LE = ΔV_V x ρ_V/ρ_L

Following thermal equilibrium, which I will assume occurs rapidly with respect to the time that the liquid is removed, the calculation cycle can be repeated using the starting conditions determined by the previous calculations, with a volume of liquid, V_L2, equal to the previous volume reduced by (ΔV_L + ΔV_LE), a new temperature equal to the previous temperature reduced by ΔT_P, and a new pressure of P_V2.

Adiabatic Results – Propane Only

These calculations were made using the above equations with the initial volume of propane of 15 gallons, and ΔV_L steps of one gallon. Initial gauge pressure was assumed to be 100 psig equivalent to 112.5 psia, corresponding to an equilibrium temperature of 62.5 ^◦F. The calculations were carried through 14 cycles, and the results are presented in Fig. 3 and Fig. 4. Thermal equilibrium was assumed to take place over the time required to removed the propane due to the short bursts of propane withdrawal and time in between bursts.

Figure 3. Calculated propane pressure vs. % propane remaining in the tank.

Propane only included in calculations.

Figure 4. Calculated propane temperature vs. % propane remaining in the tank.

Propane only included in calculations.

Another result of the calculations was that 0.42 gal. of propane was evaporated in the process of replenishing the tank with vapor as the liquid propane was used, leaving the tank with 0.58 gal. remaining after 14 cycles of the calculations.

While these results demonstrate the effect initially proposed in that the temperature and pressure of the propane decrease during operation of the balloon due to evaporation of the propane necessary to replace the volume of liquid removed during operation, the effect would be less if heat from the stainless steel tank was considered. So the next set of calculations were made to include the temperature of the tank.

Calculations of Pressure-Temperature Characteristics of Propane Fuel During the Flight of a Hot Air Balloon Assuming Adiabatic Conditions for the Propane and the Stainless Steel Tank

In the following calculations I will assume the stainless steel tank and the propane remain in thermal equilibrium under adiabatic conditions. The heat lost due to evaporation in eq. (1) is now dispersed in the propane and the stainless steel tank, and eq. (2) become

(15) ΔT_{P =} ΔH / [(V_L - ΔV_L) x C_PL x ρ_L + (V_V + ΔV_V) x C_PV x ρ_V + M_ss x C_ss]

Where M_ss is the mass of stainless steel

C_ss is the specific heat of stainless steel

In this example I used heat capacity for 304 and 321 stainless of 54.2 cal/lb-^◦C with a mass of 40 lbs. Eq. (11) for the change in temperature of the propane becomes

(16) ΔT_{P =} ΔH_L / [3.79 x {(V_L - ΔV_L) x C_PL x ρ_L + (V_V + ΔV_V) x C_PV x ρ_V} ₊ 54.2 x 40]

A new set of calculations were then performed using Eq. (10), Eq. (12) through Eq. (14), and Eq. (16) to calculate the temperature, pressure and volume of the propane including the thermal effects of the stainless steel tank. Typical values for ΔH were about 5000 cal. for each gallon of evaporated vapor, and ΔT_L ranged from about 0.5 to 7 ^◦F. The results are shown in the following figures.

Figure 5. Propane Pressure vs. % Propane Remaining for two adiabatic calculations: with propane only, and with propane and 40 lb. stainless steel tank. Initial propane pressure = 100 psig.

Figure 6. Propane Temperature vs. % Propane Remaining for two adiabatic calculations: with propane only, and with propane and 40 lb. tank. Initial propane pressure = 100 psig

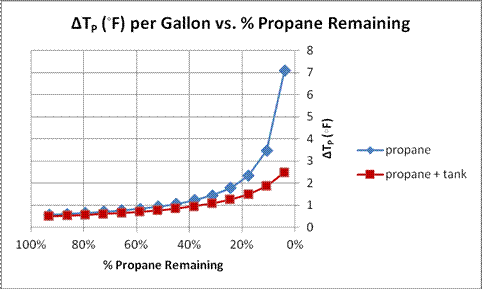
Figure 7. Change in temperature of the propane per gallon removed, ΔT_P (^◦F), vs. % Propane Remaining for two adiabatic calculations: with propane only, and with propane and 40 lb. tank. Initial propane pressure = 100 psig.

Another set of calculations was performed with an initial propane pressure of 90 psig, a starting pressure within the safe operating conditions for the balloon. Those results are presented in the next two figures.

Figure 8. Propane Pressure vs. % Propane Remaining for two adiabatic calculations: with propane only, and with propane and 40 lb. tank. Initial propane pressure = 90 psig.

Figure 9. Propane Temperature vs. % Propane Remaining for two adiabatic calculations: with propane only, and with propane and 40 lb. tank. Initial propane pressure = 90 psig.

Comparison of Calculations with Experiment (April 12, 2014)

To compare these calculations with real balloon operations, I monitored a flight on my balloon, an Aerostar S55A with vapor-converter pilot lights, on April 12, 2014. The tanks were not heated overnight because the ambient temperature had been in the low 80’s the day before, and the propane pressure remained satisfactory for the early morning flight. The flight began about 0730 with an ambient temperature of about 47 ^◦F. The propane pressure after inflation was 100 psig in both propane tanks, 15 gal., steel tanks with thermal insulation jackets. Propane pressure and percent propane in both tanks were monitored and recorded at several points during the flight. The flight was terminated at about 0840 after several take-offs and landings, one more like a “crash and drag”. One tank showed 47% propane remaining with a pressure still at 100 psig, and the other tank was at 35% with pressure of 93 psig. After tipping over the basket and detaching the envelop from the gondola, the basket was set back in the upright position, and the burner using the tank with the lower pressure was operated in several bursts over next 20 minutes until the propane level reached about 7.5% with pressure of 80 psig. At 0900 the ambient temperature had increased to 54 ^◦F. These data are summarized in the following table.

Figure 10. Recorded data for balloon flight on 4/12/2014. Note the level of propane in the tank does not register until it is less than 60%.

The data for Tank 2 are plotted in the next two figures along with the calculated results for 100 psig propane pressure in a 40-lb. steel tank. The calculated propane temperature is the equilibrium temperature based on the tank pressure as shown in Eq.(9). Note the pressure in Tank 1 did not vary over the first 70 minutes of flight, indicating that external air temperature was not a factor in the tank pressure. I failed to record the Tank 1 pressure at the end of the experiment at 0900.

Figure 11. Propane pressure vs. percent propane remaining. Experimental data during balloon flight on April 12, 2014, and calculated adiabatic results for propane in 40 lb. steel tank . The solid curves are regression trend lines calculated in a Microsoft Excel spreadsheet.

Figure 12. Calculated equilibrium temperature of the propane [Eq. (9)] for experimental flight tests and theoretical results. Also shown is the ambient temperature at beginning and end of the balloon flight.

Comparison of Calculations with Experiment (May 12, 2014)

Following the experimental balloon flight on April 12, I decided to do a more controlled experiment that was not restricted by the vagaries of a balloon flight. This entailed monitoring the propane properties during operation of the burner-propane system with the balloon gondola in a stationary position. We had flown the balloon the day before on May 11, so the propane tanks needed to be refilled. After refilling the tanks at about 3:00 pm on May 12, I began a series of operating one of the burners for Tank 1 for about five seconds every 15 to 20 seconds and monitoring the pressure at the burner. The other tank, Tank 2, and burner were not operated except for checking the pressure periodically to determine if other factors were influencing the data taken on the first burner, such as pressure changes due to non-adiabatic effects.

The data from these tests are shown in the next figure.

Figure 13. Experimental data taken on May 12, 2014.

From these data, we see that the pressure on Tank 2 remained constant indicating no impact on the propane pressure due to external thermal effects; i.e., adiabatic conditions prevailed over the time of the experiment. During operation the pressure on Tank 1 decreased from 110 psig to 85 psig as the percent propane remaining in the tank decreased from 100 percent to four percent. The calculated equilibrium propane temperature decreased from 68 ^◦F to 53 ^◦F. Ambient temperature remained constant at 62 ^◦F.

These data are plotted in the next two figures along with the theoretical calculations for an initial propane pressure of 110 psig.

Figure 14. Propane pressure vs. percent propane remaining. Experimental data and calculated adiabatic results for propane in 40 lb. steel tank . The solid curves are regression trend lines calculated in a Microsoft Excel spreadsheet. Stationary test conditions on May 12, 2014.

Figure 15. Calculated equilibrium temperature of the propane [Eq. (9)] for experimental and theoretical results. Also shown is the ambient temperature at the beginning and end of the test sequence.

These test results agree very nicely with the calculations indicating that thermal equilibrium was maintained as the burner was operated. So what is the difference between these test results and the earlier results for the balloon flight where thermal equilibrium was not achieved until the very end of the test? In the first test the propane tanks were loaded into the truck on a warm afternoon and left overnight exposed to the outside temperature which decreased from the low 80’s to 47 ^◦F. This exposure created thermal gradients in the liquid propane with warm propane at the top of the tank and cooler propane at the bottom. So during flight the colder propane at the bottom of the tank was used first leaving the warmer propane at the top which determined the vapor pressure. The propane did not reach equilibrium until the end of the test when all of the heat necessary to replenish the vapor in the tank had been extracted from the liquid. In the case of the test on May 12 , the propane had not had time to set up thermal gradients after refilling the tanks only a few minutes prior starting the tests. In this case, thermal equilibrium was maintained throughout the test.

Estimate of the Impact of Thermal Diffusion in the Liquid Propane on Balloon Performance

The difference between the experimental results and the calculations for the April 12 test is probably due to the assumption of thermal equilibrium for the liquid propane during operation. The difference narrowed as the propane level was reduced, probably because the smaller volume of propane was more closely approaching thermal equilibrium.

One explanation of the lack of equilibrium over the time scale of the balloon flight could be due to the differences in thermal diffusivity values for liquid and vapor propane, and stainless steel, about 7.5 x 10^-4 cm²/s for liquid, 6.4 x 10^-3 cm²/s for vapor, and 0.042 cm²/s for stainless. These values would indicate that the liquid would lag the other two constituents in reaching equilibrium. This can be seen in the following graphical displays of solutions to the one-dimensional diffusion equation for the different materials given by

(17) E(x,t) = Φ/(4πDt)^1/2 exp(-x²/4Dt)

where E(x,t) is energy density in the material (cal/cm³)

x is distance into material from the surface at x=0 (cm)

t is time (sec)

Φ is energy flux deposited in the material at x=0 (cal/cm²)

D is thermal diffusivity (cm²/sec)

Results for two calculations at t= 1 sec. and t=5 sec. are shown in the next two figures for the three materials, liquid propane, propane vapor and stainless steel. With about 5000 calories withdrawn with the evaporation of one gallon of vapor, the energy flux at the surface of the liquid would be about negative 5 cal./cm² with a tank diameter of 14 inches.

Fig. 13. Heat loss distribution in liquid propane, propane vapor and stainless steel at t=1 sec after removal of 5 cal/cm² at x=0 and t=0.

Fig. 14. Heat distribution in liquid propane, propane vapor and stainless steel at t=5 sec after removal of 5 cal/cm² at x=0 and t=0.

From these figures, we see in Fig. 13, in one second, the heat loss is distributed in the liquid propane to about 0.1 cm., for propane vapor about 0.2 cm, and for stainless about 0.5 cm. In Fig. 14, at five seconds, the depths respectively are about 0.2 cm, 0.5 cm and one cm. The walls to the stainless steel tank are 0.19 centimeter thick, so the heat to the wall would be conducted along the walls of the tank in a two-dimensional manner through the wall and along the vertical axis. Given the dimensions of the tank, thermal gradients would persist for much longer periods than those depicted here. The slowest to reach equilibrium would be the liquid propane. The time necessary for the propane to reach a heat loss distribution of 10% of the surface value, t_0.1, at depth d cm. can be determined using Eq. (17)

(18) E(d,t_0.1)/ E(0,t_0.1) = 0.1 = exp(-d²/4Dt_0.1) and solving for t_0.1 giving

(19) t_0.1 = 144.7 d² for the liquid propane.

Or solving Eq.(19) for d gives

(20) d = (t_0.1 / 144.7)^1/2

Applying this equation to the conditions in Fig. 14, gives d = 0.19 cm., compared to the visual estimate of about 0.2 cm.

During a 100 min. balloon flight, the heat loss in the liquid propane due to diffusion would extend only about 6.4 cm. from the liquid surface. Assuming the original height of the 15 gallons of propane in the tank to be about 30 in. or 75 cm, a gallon of propane would occupy a height of 5 cm. in the tank. So the heat removed from the propane during the flight would be concentrated in the last gallon or two left in the tank, assuming all the liquid removed came from the bottom of the tank and the heat loss due to evaporation was propagated in the liquid by diffusion. The temperature of the steel tank would be more reflective of the bulk of the liquid propane and remain higher than the surface temperature of the liquid during the early portion of the flight. The pressure in the tank would be determined by the average temperature of the propane and remain higher than would be expected based on the temperature of the liquid surface. These unbalanced temperatures are reflective of the lack of thermal equilibrium in the overall system. They would converge only near the end of the flight at low propane levels. Of course, any mixing of the liquid propane or convection currents would also reduce the thermal gradients in the propane.

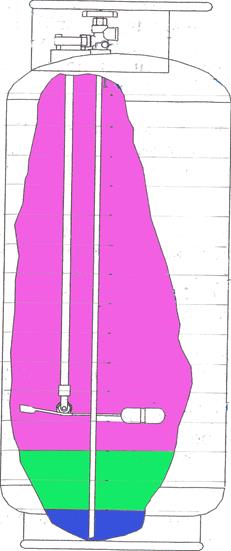
However, using this approximation is instructive in helping to understand the original test results when thermal gradients were present in the liquid prior to flight. Schematic depictions of the propane with thermal gradients in the tank are shown in Figs. 15 through 17. Figure 15 depicts the tank conditions prior to the flight; vapor is shown at the top of the tank, warm propane is shown below the vapor in the upper portion of the tank, and cool propane is depicted at the bottom. (The picture is graphic only; there would not be a sharp delineation of warm from cool propane as shown, but a gradual change over the depth of the tank). Figure 16 depicts the propane distribution when the tank is about half full. A cool layer of propane is shown at the top of the liquid due to evaporation of the vapor to fill the top half of the tank. The cool propane has been removed from the bottom and the warm propane has moved down. The pressure in the tank would reflect the warmer temperature of the propane and remain higher than it would have been without thermal gradients in the propane. Figure 17 depicts the propane near the end of the flight, where even most of the warm propane has been removed, and the cool layer at the top of the liquid is deeper than earlier in the flight. In this situation the pressure would reflect the cooler conditions of the propane and could be significantly lower than earlier in the flight. This is shown in the measurements of April 12 where the pressure remained higher than is predicted under equilibrium conditions, and dropped faster during the last part of the tests compared with the earlier time in the flight and what would have been the case with thermal equilibrium.

Cool Liquid

Warm Liquid

Vapor

Figure 15. Tank, full, with thermal gradient.

Figure 16. Tank, half full, with thermal gradient.

Figure 17. Tank, low, with thermal gradient.

Impact of Temperature and Pressure on Propane Flow Rate

The impact of temperature and pressure on propane flow can be estimated by assuming viscous flow of a liquid in a tube. The tube would consist of the coil heat exchanger between the blast valve and around the burner to the nozzle. The pressure drop through the coil is assumed to be the pressure at the valve indicated by the pressure gauge. Pressure at the outlet of the burner is assumed to be zero psig. These assumptions simplify the problem and differ somewhat from the real situation since the liquid propane is heated during the burner operation to produce vapor at the outlet, but the calculation probably gives a ball park estimate of the propane flow rate.

The mass flow rate of the liquid, R_M, in kg/sec through a tube of radius a and length L is given by

(21) R_M = (π a⁴/ 8 L) ρΔP/η

Where ΔP is the pressure drop along the tube in Pascals, ρ is the density of the liquid, and η is the viscosity of the liquid propane in Pascal-seconds. The ratio ρ/η for liquid propane at 60^◦F is 4.74 and at 50^◦F is 4.54 (kg-μPa)/(m³-sec). Thus the mass flow rate of the propane will decrease about 4% if the temperature of the liquid drops from 60^◦F to 50^◦F. Assuming the pressure drop in the burner is determined by the pressure indicated on the gauges, the experiments reported here would indicate a decrease in propane flow rate of about 20 to 25 percent during the course of a flight where most of the propane was consumed.

Conclusions

The calculations are rather simple compared to the complexity of the problem; however, the calculations and experiment support the hypothesis that propane pressure will decrease during operation of the balloon due to evaporation of the propane in the tank. The decrease in pressure and temperature over the course of a flight appears to depend to some extent on the initial conditions of the liquid propane, i.e., whether on not thermal gradients existed in the liquid prior to the flight. The pressure decrease will be accentuated at the lower levels of propane if there is a thermal gradient prior to the flight because the thermal gradient will disappear and the liquid propane will approach equilibrium conditions, an effect that was observed in the experimental flight results. In the case of initial thermal equilibrium in the liquid for the May 12 tests, the experimental results were consistent with the equilibrium calculations, where the rate of decrease in propane pressure during a flight would be more constant than the flight with the thermal gradient.

Lower initial pressure will result in lower final propane pressure and temperature. Even though a 90 psig beginning pressure is within the safe operating conditions for the balloon, calculated final pressure values at the 10% propane level fall below the recommended safe operating pressure of 80 psig.

Evaporation of the liquid in the tank reduced the volume of liquid propane by about 0.4 gal. over the 14 cycles of the calculations.

The stainless steel tank had a moderating effect on the temperature variation during the tests because of its mass and specific heat. By comparison, an aluminum tank of the same dimensions would have a smaller (about 70% of that of stainless steel) moderating effect due to its lower density combined with its higher specific heat. Titanium would have an effect of about 60% of that of stainless. So the pressure and temperature changes for these materials would be somewhere between those for the propane-only calculations and the propane-plus-tank calculations.

Vapor pilot lights will contribute to evaporation of propane in the tank and probably impact the operating conditions of the balloon in a more dramatic way at low propane levels than for balloons equipped with pilot converters operating with liquid propane. A calculation of the impact of vapor pilot lights could be made if propane flow rates were made available.

The assumption of adiabatic conditions for the propane and tank appears to be justified based on the first 70 minutes of flight data on the one tank where the percent propane did not drop to the level of impacting the tank pressure of 100 psig; i.e., the pressure decrease in tank 2 was due only to reduced propane in the tank even though the outside temperature was less than the tank temperature until the very end of the experiment. The stationary experimental results were also consistent with adiabatic conditions.

Decreases in propane pressure during the course of a flight can be over 20 per cent, indicating a corresponding reduction in propane flow rate through the burners. What might be a four second burn at the beginning of a flight to provide the correct performance of the balloon might become a five second burn at the end of the flight.

Given these calculations and measurements, a balloon pilot should be aware that when the propane in the tank is down to the last ten or fifteen percent, that propane will be cooler than the original full tank, and the pressure in the tank can drop off rather precipitously during the last few minutes of the flight if thermal gradients were present in the liquid propane prior to flight. Even though the propane pressure is still in what is considered a safe operating condition, the balloon performance could change rather suddenly in the last few minutes of the flight, especially if the flight had not been interrupted by “touch and goes” or “crash and drags” that could lead to mixing of any thermal layers in the liquid propane. The difference between operating with a 15% level in one tank compared with using the tank with a 10% level could be noticeable in the balloon performance.

Figure 18. Propane Tank. Two tanks in the balloon connected independently to each burner with high pressure hoses.

Figure 19. Dual Burner

Figure 20. Pilot Vapor Converter and Regulator; one per burner.

---

[1] In actual flight the propane to the burners is delivered in short bursts of 1-3 seconds, with time between bursts of about 10 seconds or more depending on the flight requirements. It was not practical to simulate that degree of fidelity in the calculations. ΔV of one gallon was chosen because that required only 14 cycles of calculations, and the thought was that the fidelity would be accurate enough given the assumption of thermal equilibrium over the time it takes to withdraw one gallon during flight